Un tutoriel sur l’analyse de survie à plusieurs niveaux: méthodes, modèles et applications – Austin – 2017 – Revue statistique internationale
Résumé
Les données qui ont une structure à plusieurs niveaux se retrouvent fréquemment dans une gamme de disciplines, y compris l’épidémiologie, la recherche sur les services de santé, la santé publique, l’éducation et la sociologie. Nous décrivons trois familles de modèles de régression pour l’analyse des données de survie à plusieurs niveaux. Premièrement, les modèles de risques proportionnels de Cox à effets mixtes intègrent des effets aléatoires spécifiques aux grappes qui modifient la fonction de risque de référence. Deuxièmement, les modèles de survie exponentielle par morceaux divisent la durée du suivi en intervalles mutuellement exclusifs et ajustent un modèle qui suppose que la fonction de risque est constante dans chaque intervalle. Cela équivaut à un modèle de régression de Poisson qui incorpore la durée d’exposition dans chaque intervalle. En incorporant des effets aléatoires spécifiques aux grappes, des modèles mixtes linéaires généralisés peuvent être utilisés pour analyser ces données. Troisièmement, après avoir partitionné la durée du suivi en intervalles mutuellement exclusifs, on peut utiliser des modèles de survie dans le temps discrets qui utilisent un modèle linéaire généralisé log-log complémentaire pour modéliser l’occurrence du résultat d’intérêt dans chaque intervalle. Des effets aléatoires peuvent être incorporés pour tenir compte de l’homogénéité intra-cluster des résultats. Nous illustrons l’application de ces méthodes à l’aide de données constituées de patients hospitalisés pour une crise cardiaque. Nous illustrons l’application de ces méthodes à l’aide de trois langages de programmation statistique (R, SAS et Stata).
1. Introduction
Les données avec une structure à plusieurs niveaux ou hiérarchique se produisent fréquemment dans un large éventail de disciplines de recherche. Par exemple, dans une étude sur la mortalité chez les patients hospitalisés pour une crise cardiaque, les sujets sont regroupés dans les hôpitaux, qui à leur tour peuvent être regroupés dans des régions. Un enquêteur peut être intéressé à déterminer les caractéristiques des patients, des hôpitaux et des régions associées à un risque accru de décès suite à une crise cardiaque. Dans les données conventionnelles à plusieurs niveaux, chaque unité de niveau un (par exemple, les patients) est imbriquée dans une et une seule unité de niveau deux (par exemple, les hôpitaux). Les unités de niveau deux peuvent ensuite être imbriquées dans une et une seule unité de niveau trois (par exemple, les régions). D’autres niveaux de regroupement ou d’imbrication sont possibles. Dans le didacticiel actuel, nous limitons notre attention aux données à plusieurs niveaux avec deux niveaux. Cependant, les méthodes décrites se généralisent aux paramètres avec plus de deux niveaux dans la hiérarchie des données. Le résultat ou la variable de réponse est mesuré au niveau le plus bas de la hiérarchie – sur les unités de niveau un, tandis que les variables explicatives ou prédictives peuvent être mesurées sur des unités à n’importe quel niveau de la hiérarchie.
Les modèles de régression conventionnels supposent que les sujets sont indépendants les uns des autres. Cependant, les sujets qui sont imbriqués dans la même unité de niveau supérieur sont susceptibles d’avoir des résultats corrélés entre eux, violant ainsi l’hypothèse d’observations indépendantes. Cette homogénéité au sein du cluster peut être induite par des caractéristiques de cluster non mesurées (par exemple la culture hospitalière) qui affectent le résultat ou par des covariables non mesurées au niveau du sujet (par exemple la génétique ou les pratiques diététiques lorsque les sujets sont regroupés au sein de familles) qui prennent une valeur similaire pour tous les sujets au sein du cluster. Les modèles de régression à plusieurs niveaux permettent d’analyser des données qui ont une structure à plusieurs niveaux tout en tenant compte du regroupement des unités de niveau inférieur au sein d’unités de niveau supérieur. Au cours des deux dernières décennies, les modèles multiniveaux sont passés d’une spécialité de niche (nécessitant souvent un logiciel statistique autonome spécialisé) à une partie intégrante du courant statistique (et pouvant s’adapter à l’aide de logiciels statistiques à usage général).
L’analyse de survie fait référence à des méthodes d’analyse des données dans lesquelles le résultat indique le temps écoulé avant la survenue d’un événement d’intérêt. Une caractéristique clé de l’analyse de survie est celle de la censure: l’événement peut ne pas s’être produit pour tous les sujets avant la fin de l’étude. On dit que les sujets qui sont sans événement à la fin de l’étude sont censurés. Nous renvoyons le lecteur intéressé à plusieurs des ouvrages de référence classiques sur l’analyse de survie (Cox et Oakes 1984; Kalbfleisch et Prentice 2002; Sans foi ni loi 1982; Aalen, Borgan et Gjessing 2008; Moulins 2011; Klein et Moeschberger 1997; Therneau et Grambsch 2000; Chanteur et Willett 2003). Parmi ceux-ci, un seul décrit explicitement les méthodes d’analyse des données de survie à plusieurs niveaux (Singer & Willett, 2003), tandis que trois introduisent des modèles de fragilité pour l’analyse des données de survie groupées (Therneau & Grambsch, 2000; Moulins, 2011; Aalen et coll., 2008).
Il existe un grand nombre d’ouvrages consacrés aux problématiques d’analyse des données multiniveaux (Goldstein, 2011; Raudenbush et Bryk, 2002; Snijders et Bosker, 1999; Hox et Roberts, 2011; Rabe-Hesketh et Skrondal, 2012a; 2012b). Ces livres décrivent le concept de données multiniveaux et présentent des modèles de régression appropriés pour l’analyse de ces données. Le principal objectif de bon nombre de ces livres est l’analyse des données dont le résultat est continu. Le modèle linéaire hiérarchique (HLM) est présenté comme la principale méthode d’analyse des données à plusieurs niveaux avec des résultats continus. Un objectif secondaire d’un sous-ensemble de ces livres est sur les contextes avec des résultats distincts. Le modèle linéaire généralisé hiérarchique (HGLM) est introduit pour l’analyse de données à plusieurs niveaux avec des résultats discrets. Dans la recherche appliquée, les résultats temporels surviennent fréquemment (Austin et coll., 2010). Malgré la fréquence à laquelle les résultats de survie se produisent, de nombreux ouvrages de référence complets énumérés précédemment omettent les méthodes d’analyse des données de survie à plusieurs niveaux, tandis que d’autres fournissent une discussion superficielle de l’analyse de survie à plusieurs niveaux. Un seul, qui met l’accent sur les applications utilisant Stata, fournit une discussion plus détaillée de l’analyse de survie à plusieurs niveaux (Rabe-Hesketh & Skrondal, 2012b).
L’objectif de cet article est de décrire des modèles statistiques pour l’analyse des données de survie à plusieurs niveaux. L’article est structuré comme suit: Premièrement, nous fournissons un bref examen des HGLM, car ces modèles forment la base de certains modèles statistiques pour l’analyse des données de survie à plusieurs niveaux. Deuxièmement, nous décrivons trois méthodes différentes pour l’analyse des données de survie à plusieurs niveaux. Troisièmement, nous fournissons une étude de cas illustrant l’application de ces méthodes. L’étude de cas est constituée d’une large cohorte de patients hospitalisés pour un infarctus aigu du myocarde (IAM ou crise cardiaque), qui sont nichés dans les hôpitaux dans lesquels ils ont été traités.
2 Modèles de régression logistique et de Poisson à plusieurs niveaux
Dans cette section, nous fournissons un bref aperçu des HGLM pour l’analyse de données à plusieurs niveaux lorsque le résultat est binaire ou un nombre entier. La motivation de cette revue est que deux des méthodes d’analyse des données de survie à plusieurs niveaux utilisent ces modèles.
Nous supposons que les données ont deux niveaux. Laisser Ouijejdésignent la variable de réponse binaire ou count pour le je-Th sujet imbriqué dans le j-Ème cluster. Laisser X1jej,…,Xpjej dénoter p variables explicatives qui sont mesurées sur cet individu (par exemple les caractéristiques du patient), tandis que Z1j,…,Zqjdénoter q variables explicatives mesurées sur le j-Th cluster (par exemple, caractéristiques de l’hôpital).
Un modèle de régression logistique d’interception aléatoire incorpore un seul effet aléatoire, permettant à l’interception de varier de manière aléatoire entre les grappes
, où l’on suppose que les effets aléatoires suivent une distribution normale: α0j∼N(α0,τ2). Le modèle de régression logistique des interceptions aléatoires permet à la probabilité d’occurrence du résultat pour un sujet de référence de varier d’un groupe à l’autre. Cependant, les effets des variables explicatives individuelles sont contraints d’être égaux entre les grappes. Dans un modèle de régression de Poisson à intersection aléatoire pour les résultats de comptage, le logit de la probabilité d’occurrence de l’événement est remplacé par
, où la distribution des résultats pour le je-Ème sujet dans le j-Th cluster est supposé suivre une distribution de Poisson avec moyenne μjej.
Le niveau de complexité suivant est un modèle à coefficients aléatoires, dans lequel les coefficients de régression pour les covariables au niveau du sujet peuvent varier d’un groupe à l’autre:
=α0j+α1jX1jej+ ⋯ +αpjXpjej+β1Z1j+ ⋯ +βqZqj, où l’on suppose que
. Tous les coefficients de régression pour les covariables au niveau de la matière ne doivent pas nécessairement varier d’une grappe à l’autre. On peut avoir un modèle à coefficients aléatoires dans lequel un sous-ensemble des coefficients de régression pour les covariables au niveau du sujet est contraint d’être fixé à travers les grappes, tandis que les autres sont autorisés à varier selon les grappes.
Le lecteur est renvoyé ailleurs pour un examen plus détaillé des modèles à plusieurs niveaux à utiliser avec des résultats continus ou discrets (Snijders & Bosker, 1999; Goldstein, 2011).
3 Modèles statistiques pour l’analyse de survie à plusieurs niveaux
Nous décrivons trois méthodes pour analyser les données de survie à plusieurs niveaux: les modèles de fragilité, qui sont des modèles de risque proportionnel de Cox avec des effets mixtes, des modèles de survie exponentiels par morceaux (PWE) avec des effets mixtes et des modèles de survie en temps discret avec des effets mixtes. Nous examinons successivement chacune de ces méthodes dans les sous-sections suivantes.
3.1 Modèles de fragilité: modèles de régression de Cox avec effets mixtes
Le modèle de régression des risques proportionnels de Cox est fréquemment utilisé pour l’analyse des données de survie. Un bref examen de ce modèle est fourni dans la section 1 de l’annexe A des informations complémentaires. L’inclusion d’effets aléatoires dans un modèle de risques proportionnels de Cox partage de nombreuses similitudes avec les méthodes d’analyse des données à plusieurs niveaux avec des résultats continus, binaires ou de dénombrement. Un modèle de régression conventionnel (dans ce cas, le modèle de risques proportionnels de Cox) est amélioré par l’incorporation de termes d’effets aléatoires pour tenir compte de l’homogénéité intra-cluster des résultats.
Le terme modèle de fragilité est utilisé pour désigner un modèle de régression de survie (généralement un modèle de régression à risques proportionnels de Cox ou un modèle de survie paramétrique) qui intègre des effets aléatoires. Crowther et coll. a suggéré une différenciation dans la terminologie en utilisant le terme «modèle de fragilité» pour désigner un modèle de survie avec seulement une interception aléatoire tout en utilisant le terme «modèle à effets mixtes» pour désigner un modèle qui peut avoir plusieurs effets aléatoires (Crowther, Look et Riley 2014). Ainsi, un modèle de fragilité est un cas particulier des modèles de survie à effets mixtes. Les premiers modèles de fragilité incorporaient des effets aléatoires spécifiques au sujet pour tenir compte des caractéristiques non mesurées du sujet qui influençaient le risque de survenue du résultat. Ces modèles ont ensuite été étendus aux modèles qui incorporent des effets aléatoires spécifiques aux grappes pour tenir compte de l’homogénéité au sein des grappes des résultats. Ces modèles ont été décrits comme des modèles de fragilité partagée, car le même effet aléatoire est partagé par tous les sujets au sein d’un même cluster. Dans cet article du didacticiel, nous nous concentrons sur l’inclusion d’effets aléatoires dans le modèle de régression à risque proportionnel de Cox, en raison de la fréquence relative avec laquelle ce modèle est utilisé. Lorsque des effets aléatoires sont incorporés dans le modèle de Cox, ces effets aléatoires dénotent un risque accru ou réduit pour des classes distinctes (par exemple, des grappes telles que les hôpitaux, les écoles ou les lieux de travail).
Supposons que les sujets sont imbriqués dans l’une des classes ou groupes M (par exemple les hôpitaux). Un modèle de Cox avec des effets mixtes peut être formulé comme
, où αj désigne l’effet aléatoire associé au j-Ème cluster. Rabe-Hesketh et Skrondal utilisent le terme «fragilité partagée» pour désigner l’exponentielle de l’effet aléatoire:
(Rabe-Hesketh et Skrondal, 2012b). L’effet aléatoire peut être considéré comme une interception aléatoire qui modifie le prédicteur linéaire, tandis que le terme de fragilité partagé a un effet multiplicatif sur la fonction de risque de base:
.
Les modèles de régression de Cox à effets mixtes sont caractérisés par la distribution des termes de fragilité partagés. Différentes distributions ont été proposées pour la distribution des termes de fragilité partagés, y compris la distribution gamma, la distribution log-normale (les termes de fragilité auront une distribution log-normale tandis que les effets aléatoires auront une distribution normale), des distributions de fragilité stables positives et distributions des fonctions de variance de puissance (Hougaard, 2000; Wienke, 2011; Duchateau et Janssen, 2008). Les deux premiers semblent être les plus couramment utilisés. Dans le modèle de fragilité gamma, les effets aléatoires spécifiques à la grappe sont distribués sous forme de logarithmes de variables aléatoires gamma indépendantes, distribuées de manière identique, ayant une variance θ. La corrélation intra-cluster des sujets est
. Nous renvoyons le lecteur intéressé à des discussions approfondies sur les modèles de fragilité (Wienke, 2011; Hougaard, 2000; Duchateau et Janssen, 2008).
Dans les HLM ou HGLM conventionnels, on suppose presque toujours que les effets aléatoires suivent une distribution normale. Cependant, les chercheurs utilisant des modèles de survie avec des termes de fragilité ont plusieurs distributions parmi lesquelles choisir pour la distribution des termes de fragilité partagés. Il y a peu de conseils sur la façon de choisir entre différentes familles fragiles. Les méthodes de choix entre les distributions de fragilité sont examinées dans la section 2 de l’annexe A des informations complémentaires.
Les modèles de régression de Cox à effets mixtes ressemblent aux HGLM décrits précédemment. Les termes d’effets aléatoires spécifiques aux grappes ont un effet relatif sur la fonction de risque de base. Par conséquent, l’effet relatif d’un modèle de covariable donné sur la fonction de risque de base varie d’un groupe à l’autre. En raison de cette similitude entre les modèles de fragilité partagés HLM / HGLM et Cox, ces modèles sont une approche intéressante pour adapter les modèles de survie aux données à plusieurs niveaux. Comme avec les HLM / HGLM, les modèles Cox avec des effets mixtes ne sont pas limités à une utilisation avec des données avec un seul niveau de clustering. Rondeau et coll. utiliser le terme «modèle de fragilité imbriquée» pour désigner des modèles de survie à effets aléatoires dans lesquels il existe au moins deux niveaux de regroupement (Rondeau, Mazroui & Gonzalez 2012). Cependant, il existe certaines limites à l’utilisation des modèles de Cox avec des effets mixtes. Premièrement, les modèles de fragilité partagés de Cox nécessitent l’hypothèse que chaque sujet est membre d’une seule unité de niveau deux, donc on ne peut pas rendre compte de structures à plusieurs niveaux plus complexes telles que les données à plusieurs niveaux à appartenance multiple, dans lesquelles certains sujets sont regroupés à plus d’un niveau. deux unités (Therneau & Grambsch, 2000). Deuxièmement, alors que les modèles de Cox à effets mixtes peuvent être étendus pour prendre en compte les données à plusieurs niveaux avec plus de deux niveaux (par exemple, les données dans lesquelles les unités de niveau un sont regroupées dans des unités de niveau deux, qui à leur tour sont regroupées dans des unités de niveau trois), ces extensions ont n’a pas été intégré dans de nombreux logiciels statistiques populaires.
3.2 Modèles de survie exponentielle par morceaux avec effets mixtes
Lorsqu’on utilise un modèle de risques proportionnels de Cox, on est libéré de la nécessité de spécifier la distribution de la fonction de danger (ou de manière équivalente, de la spécification de la distribution des temps d’événements). Dans les modèles de survie paramétriques, l’analyste doit formuler des hypothèses spécifiques sur la forme de la fonction de risque. Les modèles de survie paramétriques couramment utilisés incluent le modèle de survie exponentielle (dans lequel la fonction de risque est supposée constante dans le temps: h(t) =λ) et le modèle de survie de Weibull (dans lequel la fonction de hasard est de la forme h(t) =λγtγ−1, avec λ et γ désignant respectivement les paramètres d’échelle et de forme).
Le modèle PWE est un modèle de survie dans lequel l’échelle de temps est divisée en intervalles et la fonction de risque est supposée constante dans chaque intervalle (Allison, 2010). Ainsi, on peut définir un ensemble de K intervalles, définis par K + 1 points de coupure: τ0,τ1,…, τK, (où τ0= 0 et
. Dans l’intervalle k, donné par[[[[τk − 1,τk), la fonction de danger pour un sujet donné est supposée constante et est liée à la fonction de danger de base par la fonction
, où λk est la fonction de risque de base dans le k-Ème intervalle. En construisant les intervalles, Allison suggère qu’il y a un certain avantage à avoir un nombre approximativement égal d’événements se produisant dans chaque intervalle (Allison, 2010). Par conséquent, les intervalles n’ont pas besoin d’être de la même longueur. Alternativement, on peut sélectionner les intervalles en utilisant la connaissance du sujet de telle manière qu’il soit raisonnable de croire que le danger est constant dans chaque intervalle. Des exemples d’applications du modèle PWE sont fournis par Breslow (1974), Whitehead (1980) et Aitkin et coll. (1983). Sous certaines hypothèses, des coefficients de régression équivalents à ceux obtenus à partir d’un modèle à risques proportionnels de Cox peuvent être obtenus à partir d’un modèle de survie dans lequel on suppose que la fonction de hasard est constante entre des moments d’événements successifs (Breslow, 1974; Laird et Olivier, 1981). Ainsi, le modèle de risques proportionnels de Cox peut être considéré comme le cas limite du modèle PWE.
Si la fonction de danger est constante en fonction du temps (i.e. λ(t) =λ), alors le modèle de survie exponentielle et le modèle de régression de Poisson peuvent être utilisés de manière interchangeable (Laird & Olivier, 1981). Par conséquent, le modèle PWE équivaut à un modèle de régression de Poisson (Rodriguez, 2008; Goldstein, 2011). Compte tenu des données de survie consistant en un temps de survie observé (éventuellement censuré) tje pour le je-Ème sujet et un indicateur d’événement réje indiquant si l’événement a été observé pendant le je-Ème sujet (réje= 1 désignant l’événement survenu, 0 sinon), on peut définir des mesures analogues pour chaque intervalle de durée (Rodriguez, 2008). Donc tjej désigne le temps de survie pour le je-Ème sujet dans le j-Ème intervalle, et réjej est un indicateur d’événement qui prend la valeur 1 si le je-Le sujet a vécu l’événement dans l’intervalle j, et prend la valeur 0 sinon. Un modèle PWE peut s’adapter en traitant les indicateurs d’événements comme s’il s’agissait d’observations de Poisson avec des moyennes μjej=λjejtjej, où λjejest le danger pour le je-Th individu dans le j-Ème intervalle. Ce faisant, il faudrait incorporer une variable de décalage indiquant le logarithme du temps à risque pendant chacun des intervalles (Crowther et coll., 2012).
Comme indiqué précédemment, le cadre théorique et le logiciel statistique sont plus matures pour la formulation et l’ajustement des HLM et des HGLM. Le fait que l’on puisse ajuster un modèle de survie PWE en utilisant un modèle linéaire généralisé (c’est-à-dire un modèle de régression de Poisson) a des conséquences importantes pour l’ajustement des modèles de survie à plusieurs niveaux. Premièrement, on peut incorporer des interceptions aléatoires spécifiques au cluster pour incorporer l’homogénéité au sein du cluster dans les résultats. Comme pour les HLM et HGLM, on n’est pas limité à une hiérarchie de données à deux niveaux, avec une seule source de clustering. Au contraire, on peut développer des modèles à plusieurs niveaux avec plus de deux niveaux de clustering. Deuxièmement, alors que l’utilisation de modèles de Cox avec effets aléatoires permet à la fonction de risque de base de varier selon les grappes, l’utilisation d’un modèle de régression de Poisson à coefficients aléatoires permet à l’effet d’une covariable donnée de varier selon les grappes. Les coefficients aléatoires sont plus facilement incorporés en utilisant cette approche qu’avec le modèle de Cox à effets mixtes. Troisièmement, en utilisant le modèle PWE et en incorporant des effets aléatoires, on peut utiliser des procédures statistiques disponibles dans de nombreux logiciels statistiques populaires (par exemple R, SAS et Stata).
3.3 Modèles de survie en temps discret avec effets mixtes
Des modèles de survie en temps discret peuvent être utilisés lorsque le temps de survie est mesuré en valeurs discrètes (par exemple, années jusqu’à l’incidence de la maladie). Ces modèles utilisent une version discrète de la fonction de danger. Les modèles de régression binomiale, avec une fonction de lien logit, probit ou complémentaire log – log, peuvent être utilisés pour modéliser la probabilité que l’événement se soit produit à un moment précis, à condition qu’il ne se soit pas encore produit (Rabe-Hesketh & Skrondal , 2012b). Même lorsque le temps de survie est (approximativement) continu, le modèle de survie en temps discret peut être utilisé en divisant le temps de survie en un nombre fini d’intervalles discrets. Le modèle de survie PWE décrit plus haut a divisé l’échelle de temps en une séquence d’intervalles, en supposant que la fonction de risque était constante à l’intérieur de chacun de ces intervalles. Lors de l’ajustement du modèle de survie PWE, la durée d’exposition (ou le temps à risque) de chaque sujet pendant l’intervalle est prise en compte (en tant que variable de décalage). Les modèles de survie en temps discret utilisent une approche similaire; cependant, on note simplement si un événement s’est produit ou non dans l’intervalle donné et ne tient pas compte de la durée d’exposition de chaque sujet dans l’intervalle donné. Un modèle de régression pour les résultats binaires peut ensuite être utilisé pour modéliser la probabilité d’occurrence d’un événement dans chaque intervalle. Les fonctions de lien possibles pour le modèle linéaire généralisé sont la fonction de lien logit, la fonction de lien probit et la fonction de lien log – log complémentaire (Rodriguez, 2008; Allison, 2010; Goldstein, 2011). Un avantage de ce dernier est que les coefficients de régression résultants sont identiques à ceux d’un modèle de régression à risques proportionnels sous-jacent (Allison, 2010; Rabe-Hesketh et Skrondal, 2012b). Ainsi, les coefficients estimés peuvent être interprétés comme ayant un effet relatif sur le risque de survenue de l’événement. Un avantage des modèles de survie en temps discret par rapport au modèle de survie PWE est qu’il n’est pas nécessaire de faire l’hypothèse que la fonction de risque est constante dans chaque intervalle.
Les modèles de survie en temps discret peuvent facilement incorporer la structure à plusieurs niveaux des données. Comme on ajuste un HGLM (un modèle binomial avec une fonction de lien logit ou une fonction de lien log – log complémentaire), des méthodes statistiques standard et des logiciels pour les HGLM peuvent être employés. Des discussions détaillées sur les modèles de temps discrets à plusieurs niveaux sont fournies par Steele (2011), par Barber et coll. (2000) et par Rabe ‐ Hesketh & Skrondal (2012b). Comme pour le modèle de survie à effets mixtes PWE, des coefficients aléatoires peuvent être facilement incorporés en incluant des coefficients aléatoires dans le HGLM en cours d’ajustement.
4 Étude de cas
4.1 Question de recherche
Nous avons cherché à répondre à deux questions de recherche principales. La première question était plus générale: quelles caractéristiques du patient et de l’hôpital augmentent le risque de décès suite à une hospitalisation pour IAM. La deuxième question portait sur une caractéristique spécifique du patient: la présence d’un choc cardiogénique à l’arrivée à l’hôpital (une condition dans laquelle le cœur ne pompe pas correctement, avec une chute de la pression artérielle qui s’ensuit, ce qui peut entraîner une perte de conscience du patient). Nous avons cherché à répondre à deux questions spécifiques liées au choc cardiogénique: (i) Dans quelle mesure la présence d’un choc cardiogénique augmente-t-elle le risque de décès chez les patients hospitalisés avec une IAM? (ii) L’ampleur de l’effet du choc cardiogénique sur le risque de décès varie-t-elle d’un hôpital à l’autre?
4.2 Données
Nous illustrons l’analyse des données de survie à plusieurs niveaux à l’aide des données de la base de données sur l’infarctus du myocarde de l’Ontario, qui contient des informations sur les patients hospitalisés avec un diagnostic d’IAM dans les hôpitaux de l’Ontario entre 1992 et 2013. Détails sur sa construction en reliant différentes bases de données administratives de soins de santé fournies ailleurs (Tu , Austin et Naylor 1999) (la base de données est mise à jour annuellement, elle contient donc des données pour des années au-delà de celles décrites dans la description initiale). Pour nos analyses, nous avons utilisé les sorties de l’hôpital (sorties survenues soit en raison de la sortie d’un patient, soit d’un décès à l’hôpital) survenues au cours de la période de 12 mois entre le 1er avril 2005 et le 31 mars 2006. Pour chaque patient, nous avons noté l’identité de l’hôpital dans lequel le patient a été admis. Les données ont une structure hiérarchique, les patients étant imbriqués dans les hôpitaux. L’échantillon de l’étude était composé de 16 985 patients traités dans 164 hôpitaux. L’échantillon était composé de patients uniques: en raison des critères d’inclusion et d’exclusion de l’étude, aucun patient n’a eu plus d’une sortie d’hôpital au cours de la période d’un an de l’étude.
Les variables ont été mesurées aux deux niveaux de la hiérarchie. Les variables au niveau des patients comprenaient les onze variables du modèle de prédiction de la mortalité par AMI de l’Ontario (âge, sexe, insuffisance cardiaque congestive, choc cardiogénique, arythmie, œdème pulmonaire, diabète sucré avec complications, accident vasculaire cérébral, maladie rénale aiguë, maladie rénale chronique et tumeur maligne) (Tu et coll., 2001). Les variables au niveau de l’hôpital comprenaient l’hôpital universitaire universitaire (vs hôpital non universitaire), le volume d’IMA de l’hôpital au cours de l’année précédant l’étude et la capacité hospitalière pour les procédures cardiaques invasives (classées comme revascularisation (intervention coronarienne percutanée ou pontage coronarien) capacité versus capacité de cathétérisme cardiaque (angiographie coronarienne) versus absence de capacité pour les procédures invasives). Les deux variables explicatives continues (âge et volume d’IMA de l’hôpital) étaient chacune centrées autour de la moyenne de l’échantillon pour cette variable. Les noms de variable indiqués dans la sortie du logiciel statistique sont décrits dans la section 3 de l’annexe A des informations complémentaires.
Le résultat au niveau des patients pour l’étude de cas était le temps écoulé entre l’admission à l’hôpital et le décès, quelle qu’en soit la cause. Les patients ont été suivis jusqu’à 30 jours à compter de leur admission à l’hôpital et ont été censurés après 30 jours de suivi s’ils étaient encore en vie. Le décès dans les 30 jours suivant l’hospitalisation est survenu chez 2 107 (12,4%) patients de l’échantillon de l’étude.
4.3 Logiciel statistique
Les analyses de notre étude de cas ont utilisé trois logiciels statistiques différents: R (version 3.0.2), SAS (version 9.3) et Stata (version 13.1). Les packages R suivants ont été utilisés: survival (version 2.38‐2), lme4 (version 1.1‐7) et coxme (version 2.2‐3). Deux fonctions Stata, mepoisson et mecloglog, ont été utilisées qui n’étaient pas disponibles dans les versions antérieures de Stata. Le code logiciel statistique en R, SAS et Stata est fourni à l’annexe B des informations complémentaires pour toutes les analyses. Les résultats de certaines analyses sont rapportés dans le texte; cependant, pour réduire les redondances, certaines sorties sont signalées à l’annexe C des informations complémentaires.
4.4 Modèles statistiques pour les données de survie à plusieurs niveaux
4.4.1 Modèles de Cox avec effets mixtes
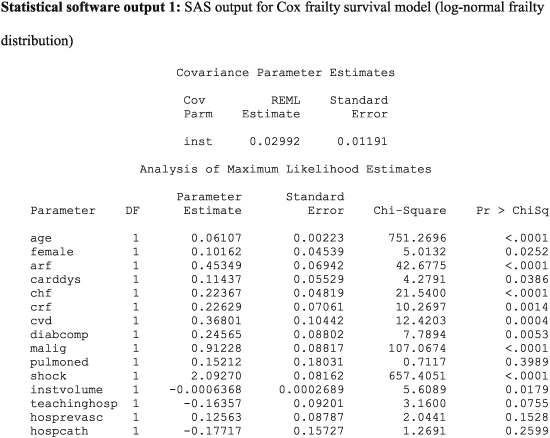
Les estimations des paramètres rapportées dans la sortie 1 du logiciel statistique sont des rapports de risque logarithmique. Les exponéner produit des rapports de risque. Ainsi, le rapport de risque du choc cardiogénique est exp (2,09270) = 8,11. Par conséquent, la présence d’un choc cardiogénique augmente le risque de décès d’un facteur huit par rapport aux sujets sans choc cardiogénique. En examinant les résultats, on observe que, à l’exception de l’œdème pulmonaire, toutes les caractéristiques au niveau du patient sont associées au risque de mortalité (P<0,039). Cela fournit une réponse au premier élément de notre question de recherche spécifique.
L’augmentation de l’âge des patients, du sexe féminin et la présence de huit des neuf facteurs de risque ont augmenté le risque de mortalité post ‐ IAM. L’augmentation du volume hospitalier est associée à une diminution du risque de mortalité (P= 0,018). Le risque relatif pour une augmentation du volume hospitalier de 100 patients est égal à exp (100 × −0,0006368) = 0,94. Ainsi, une augmentation du volume hospitalier de 100 patients est associée à une diminution de 6% du taux de mortalité des patients. L’effet de l’affiliation universitaire de l’hôpital et la présence des capacités pour les procédures invasives ne sont pas statistiquement significativement différents de zéro (P> 0,075). Ces observations apportent des réponses à notre première question de recherche générale.
La sortie SAS pour le modèle de fragilité gamma est rapportée à l’annexe C dans les informations complémentaires, dans la sortie logicielle statistique C1. L’estimation de θ, la variance de la distribution de fragilité, était de 0,02443. Comme décrit précédemment,
est une estimation de la corrélation intra-cluster des résultats. Ainsi, la corrélation intra-cluster des temps de survie est légèrement supérieure à 0,01. Les estimations des paramètres et les niveaux de signification statistique étaient très similaires entre le modèle de fragilité gamma partagée et le modèle de fragilité partagée log-normale estimé à l’aide de SAS. Les résultats du modèle de fragilité partagée log-normale estimé à l’aide de R, le modèle de fragilité partagée gamma estimé à l’aide de R et le modèle de fragilité partagée gamma estimé à l’aide de Stata sont présentés dans les sorties logicielles statistiques C2, C3 et C4, respectivement, à l’annexe C Information. Les modèles équipés de R et SAS étaient très similaires les uns aux autres. En général, les coefficients de régression pour le modèle de fragilité gamma estimé à l’aide de Stata étaient très similaires à ceux des modèles de fragilité gamma estimés à l’aide de R ou SAS; cependant, il y avait quelques exceptions où il y avait des différences significatives dans les rapports de risque estimés. Par exemple, dans le modèle de fragilité gamma estimé à l’aide de SAS, le rapport de risque pour le choc était de 8,12 (= exp (2,09449)), alors que le rapport de risque correspondant pour le modèle de fragilité gamma estimé à l’aide de Stata était de 6,0303. De même, il y avait une variable avec un niveau de signification statistique qualitativement différent entre les logiciels. L’effet du sexe du patient était statistiquement significativement différent de nul dans le modèle de fragilité gamma estimé en utilisant à la fois SAS et R (P= 0,025 dans les deux packages), alors que le rapport de risque estimé n’était pas statistiquement significativement différent de nul dans le modèle de fragilité gamma estimé à l’aide de Stata (P= 0,160). Hormis cette incohérence, des conclusions qualitativement similaires sur la signification statistique ont été obtenues à partir des différents logiciels statistiques.
Dans R, une alternative à l’utilisation de la fonction coxph est l’utilisation de la fonction coxme du package coxme ou de la fonction fragilityPenal du package frailtypack. Ces fonctions alternatives peuvent être utilisées pour ajuster les modèles de Cox avec deux ensembles différents d’effets aléatoires.
The variation in the hazard and survival functions for a reference subject across hospitals is described in Figure 1. A reference patient was a subject all of whose covariates were equal to zero (i.e. a male patient of average age, with no comorbidities, admitted to a non‐teaching hospital with average AMI volume and that had no capacity for invasive cardiac procedures). These figures were derived from the frailty model fitted in R that assumed a log‐normal distribution for the shared frailty distribution. The left panel depicts variation in the hazard function for this reference patient across hospitals. The upper two lines represent hospitals whose random effects were one and two standard deviations higher than average, the lower two lines represent hospitals whose frailties were one and two standard deviations lower than average, and the middle one represents an average hospital (with a frailty of zero). The right panel depicts the survival curves for a reference patient at these five hospitals. Note that the ordering of the curves is reversed in this figure: a hospital with a relatively lower hazard of death will have a relatively higher survival function. We observe that the hazard of death is greatest in the period immediately after admission and then declines over time. In the right panel, we observe meaningful differences in survival between these hospitals. The difference in the 30‐day survival probabilities between a hospital whose random effect was one standard deviation higher than average and a hospital whose random effect was one standard deviation lower than average was 0.028. The reciprocal of this difference is equal to 35.7, which is equal to the number needed to treat; one would need to move 36 patients from a hospital whose random effect was one standard deviation higher to a hospital whose random effect was one standard deviation lower to avoid one death within 30 days of hospital admission (Altman & Andersen, 1999).
4.4.2 Piecewise exponential model with mixed effects
In consultation with a cardiovascular expert, we divided the maximum duration of follow‐up into five strata such that it would be reasonable to assume that the hazard of death post‐AMI was approximately constant within each interval. The intervals were as follows: [0,2), [2,5), [5,10), [10,20) and [20,30]. For the purposes of the subsequent analyses, we assumed that the hazard of death post‐AMI was constant within each of these time intervals.
Fitting the PWE model required that the dataset be restructured. The dataset was modified so that there was one record corresponding to each of the aforementioned time intervals in which the patient was alive. Thus, if a patient died on day 24, the rows of data for this subject would be as follows (note: the following data are purely hypothetical and are used for illustrative purposes only):
| Id | interval | start_time | end_time | at_risk_time | event | age |
| 1 | 1 | 0 | 2 | 2 | 0 | 65 |
| 1 | 2 | 2 | 5 | 3 | 0 | 65 |
| 1 | 3 | 5 | dix | 5 | 0 | 65 |
| 1 | 4 | dix | 20 | dix | 0 | 65 |
| 1 | 5 | 20 | 24 | 4 | 1 | 65 |
Fitting the PWE model requires creating an offset variable that is equal to the logarithm of the duration of exposure within each window. Because survival time was measured in integer values of days, there was a non‐zero probability that a patient would die at the beginning of the interval, resulting in an exposure time of zero and an offset variable that is undefined. When this occurred, subjects were defined to have an exposure duration of 0.5 days (i.e. assuming that they died in the middle of the day) and an offset variable of log(0.5). In R, the survSplit function in the survival package can be used to structure the dataset appropriately, while in Stata, the stsplit function can be used. In SAS, to the best of our knowledge, programming using data steps must be used to create the necessary dataset.
Output for the PWE survival model estimated using R and SAS is reported in Statistical software output C5 and C6, respectively, in Appendix C in the Supporting Information. Estimated regression coefficients and levels of statistical significance are similar across the three statistical software packages. In Stata, the estimate of the variance of the random effect distribution is 0.0256063, while in SAS and R, the estimated variance of the random effects were 0.02578 and 0.02563, respectively. Note that when treating the time interval as a categorical variable, SAS chooses the last interval as the reference level for the categorical variable, while R and Stata choose the first interval as the reference level for the categorical variable. Thus, the estimated intercept and regression coefficients for the non‐reference levels of the time interval variable differ between the model estimated using SAS and the models estimated using R and Stata.
Hazard functions for a reference patient (similar to the one described earlier) for an average hospital and for hospitals whose random effect was one or two standard deviations above or below the average are depicted in Figure 2. These figures were based on the results of the PWE model fit in R. If the PWE model is fit without an intercept and if indicator variables for each of the time intervals are included, then the exponentiated regression coefficient for each time interval is the constant hazard within that interval (Rabe‐Hesketh & Skrondal, 2012b). The model described earlier was refitted using this specification to estimate the hazard function (results not shown). One notes that the absolute differences in the hazard of death between different hospitals decrease as time progresses: the greatest differences in the hazard of death between hospitals occurs in the period immediately after hospital admission.
4.4.3 Discrete time mixed effects model
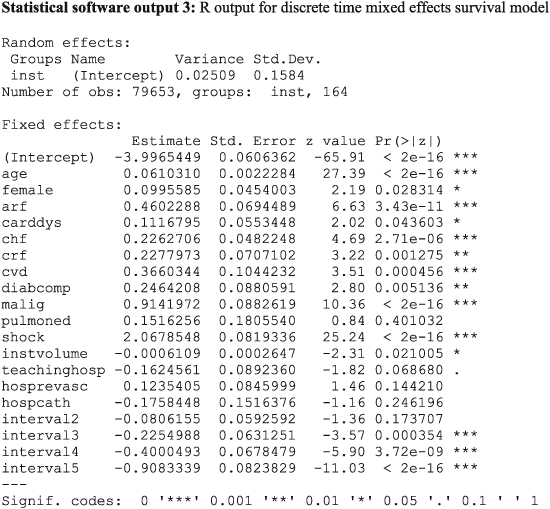
The output for the discrete time mixed effects survival model fit using SAS and Stata is reported in Statistical software output C7 and Statistical software output C8, respectively, in Appendix C in the Supporting Information. Estimated regression coefficients and level of statistical significance for the discrete time survival model were similar between the three statistical software packages. The estimated variance of the random effect distribution was 0.02509, 0.02258 and 0.0250974 when using R, SAS, and Stata, respectively.
Increasing patient age, female sex and the presence of seven of the nine risk factors increased the hazard of post‐AMI mortality. In all three models, pulmonary edema was not associated with the hazard of post‐AMI mortality. When the model was fit using SAS, the presence of cardiac dysrhythmia was not associated with the hazard of death (P=0.060 ), while it had a statistically significant association in the models estimated in R (P=0.044 ) and Stata (P=0.044 ). Of the measured hospital characteristics, only hospital volume of AMI patients was associated with a decreased hazard of mortality, while the other hospital characteristics did not have a statistically significant association with the hazard of mortality.
4.4.4 Random coefficients models
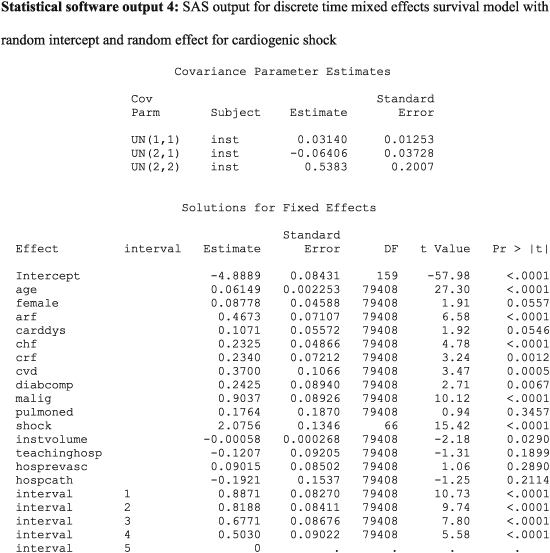
In the above output, more than one random effect covariance parameter is reported. For the above model, three variance–covariance terms are reported: 0.03140, −0.06406 and 0.5383. The first (0.0314) denotes the variance of the random intercepts across hospitals. The last (0.5383) denotes the variance of the random slope for cardiogenic shock across hospitals. The second term (−0.06406) denotes the covariance between these two random effects. The covariance term is negative, denoting a negative correlation between the hospital‐specific random intercepts and the hospital‐specific random slopes for cardiogenic shock. The correlation between random intercepts and slopes is equal to
. Thus, hospitals that have a higher intercept (increased hazard of death for a reference patient) will tend to have a diminished effect of cardiogenic shock on death.
The hazard ratio for cardiogenic shock at an average hospital is exp(2.0756) = 7.97. Thus, at an average hospital, the presence of cardiogenic shock increases the rate of death by a factor of almost eight. Ninety‐five percent of hospitals have a log‐hazard ratio for cardiogenic shock that lies within the interval
. By taking the endpoints of this interval to the power e, one concludes that 95 percent of hospitals have a hazard ratio for cardiogenic shock that lies in the interval (1.89, 33.58). Thus, while the presence of cardiogenic shock increases the risk of death at the large majority of hospitals, there is a small minority of hospitals at which its presence is particularly lethal. This provides an answer to the second component of our specific research question: the magnitude of the effect of cardiogenic shock varies across hospitals.
The output for the Cox model with mixed effects fit using R is reported in Statistical software output C9 in Appendix C in the Supporting Information.
5 Discussion
Time‐to‐event outcomes occur frequently across a wide range of fields of research. Multilevel data are common in many of these research fields. While HLMs and HGLMs are well known and used frequently for the analysis of multilevel data with continuous or discrete outcomes, methods for the analysis of multilevel survival data are less well known. The objective of this article is to describe statistical methods for analysing multilevel survival data.
We described three different families of models that allow one to fit survival models to multilevel data: Cox regression models with mixed effects, PWE models with mixed effects, and discrete time survival models with mixed effects. The first approach modifies a Cox proportional hazards regression model by incorporating cluster‐specific random effects that modify the baseline hazard function. The second approach divides follow‐up time into a finite set of mutually exclusive intervals and fits a survival model that assumes that the hazard function is constant within each interval (equivalent to assuming that survival times follow an exponential distribution within each interval). This approach makes use of the fact that an exponential survival model is equivalent to a Poisson regression model. Thus, one can account for the multilevel structure of the data by fitting a Poisson regression model within each time interval and incorporating cluster‐specific random effects. The third approach is similar to the second. However, rather than taking into account the duration of exposure time or at‐risk time within each interval, one simply notes whether the subject experienced an event within the given interval. Then a complementary log–log generalised linear model can be fit. As with the PWE model, cluster‐specific random effects can be incorporated to account for the multilevel structure of the data.
Relative strengths and limitations of each method are summarised in Table 1. We provide some recommendations for applied analysts when choosing between the models. If the data consist of a two‐level multilevel structure, and one simply wants to account for clustering (and possibly to describe the magnitude of the effect of clustering), we recommend that the Cox model with random shared frailty terms be used. This method requires weaker assumptions than the PWE model. Furthermore, it does not require restructuring the dataset and dividing follow‐up time into discrete intervals. Such a discretisation process can result in a loss of information. Furthermore, when a Cox model with random shared frailty terms is fit, one can use the median hazard ratio as a measure of the magnitude of the effect of clustering on the hazard of the outcome (Austin et coll., 2017) However, several popular statistical analysis packages currently appear to be unable to fit a Cox model with random frailty terms to data in which there are more than two levels to the data hierarchy. Furthermore, the Cox shared frailty model requires that each subject be a member of only one level two unit. Thus, one cannot fit this model to multilevel multi‐membership data. Users of some statistical software packages whose research question requires them to fit models with random coefficients (e.g. to examine whether the effect of a given covariate varies across clusters) may be required to choose between the PWE and the discrete time model because the Cox model with random coefficients currently cannot be fit in all popular statistical software packages. Of these two models, the PWE requires the stronger assumption that the hazard function is constant within each time interval. However, the PWE model accounts for the duration of at‐risk time within each time interval, whereas the discrete time model simply models whether or not an event occurred during each time interval. Thus, an analyst who had data consisting of more than two levels or who wanted to fit a model with random coefficients may be required to consider either the PWE model or the discrete time model. Strengths and limitations of three popular statistical analysis packages (R, SAS and Stata) are described in Section 4 of Appendix A in the Supporting Information.
Strengths and limitation of each statistical model.
| Model | Strengths | Limitations | ||
|---|---|---|---|---|
| Cox model with mixed effects | • | Can easily incorporate shared frailty terms using standard software for the Cox model. | • | Random coefficients cannot currently be incorporated in some software packages. |
| • | Allows hazard function to vary continuously. | • | Limited information on how to choose between different frailty distributions. | |
| • | Familiar to researchers in the epidemiological and biomedical literature. | |||
| PWE model | • | Can be fit using software for fitting HGLMs. | • | Requires dividing follow‐up time into discrete intervals with the assumption that the hazard function is constant within each interval. This may not be a realistic assumption in all settings. |
| • | Can easily incorporate random coefficients using standard software for HGLMs. | • | Little research on sensitivity to choice of time intervals. | |
| • | May be more familiar to researchers in the social and behavioural sciences. | • | Dataset must be restructured. | |
| Discrete time model | • | Can be fit using software for fitting HGLMs. | • | Requires dividing follow‐up time into discrete intervals. |
| • | Can easily incorporate random coefficients using standard software for HGLMs. | • | Does not take the duration of time at‐risk within each interval. | |
| • | Regression coefficients are identical to those of an underlying proportional hazards regression model. | • | Little research on sensitivity to choice of time intervals. | |
| • | May be more familiar to researchers in the social and behavioural sciences. | • | Dataset must be restructured. |
- PWE, piecewise exponential; HGLM, hierarchal generalised linear model.
We described three different families of models for the analysis of multilevel survival data: Cox proportional hazards regression models with mixed effects, PWE survival models with mixed effects and discrete time survival models with mixed effects. While we have presented these as three distinct families, they are related to one another. The Cox proportional hazards model with gamma frailty is equivalent to the PWE survival model in which intervals are defined so that there is one event per interval and that incorporates cluster‐specific random effects (Rabe‐Hesketh & Skrondal, 2012b) (Section 15.9, page 843). Similarly, the complementary log–log discrete time survival model is an approximation to the PWE survival model. The approximation improves as the intervals become narrower (Steele, 2011) (page 5). Consequently, a complementary log–log discrete time survival model with random intercepts will be approximately equivalent to a Cox proportional hazards model with log‐normal frailty terms.
In the current tutorial, we focused on models that incorporated random effects to account for within‐cluster homogeneity of outcomes. These methods explicitly model the between‐cluster variability in the hazard of the occurrence of an outcome. We did not discuss methods that did not explicitly incorporate cluster‐specific random effects for accounting for within‐cluster homogeneity. Accordingly, our focus was on conditional models, rather than on marginal models. When using marginal models with a two‐level data structure, one could use a robust or sandwich‐type variance estimator to account for the clustering of subjects (Lin & Wei, 1989). However, this approach can lead to loss of information, as one is not explicitly modelling between‐cluster variability. An example of a consequence of this is that one cannot describe variation in the conditional hazard function across clusters. It is important to note that the regression coefficients derived from conditional and marginal models have different interpretations. Regression coefficients from the former family have a conditional interpretation: an estimated regression coefficient denotes the effect of a covariate on the hazard of the occurrence of the outcome conditional on tous les deux the random effect being fixed or constant et on the other covariates being fixed. For this reason, the coefficients are sometimes described as having a cluster‐specific interpretation. Regression coefficients from a marginal model have a population‐average interpretation; an estimated regression coefficient denotes the effect of the covariate comparing two random sample of subjects such that the two samples differ in the value of the covariate by one unit (and all other covariates are fixed) (Therneau & Grambsch, 2000). In general, marginal hazard ratios will be closer to the null than conditional hazard ratios (Gail, Wieand & Piantadosi 1984). A limitation to the use of marginal models is that it is more difficult to account for clustering when the data have more than two levels, whereas such data structures can be readily accommodated with conditional survival models.
In the current paper, we have discussed methods for the analysis of multilevel survival data. Our descriptions have been set in the context of a two‐level data structure (e.g. patients nested within hospitals). However, all of the methods can be extended to data in which there are more than one level of clustering (e.g. patients nested within physicians who are in turn nested within hospitals). When using the PWE survival model with mixed effects or the discrete time survival model with mixed effects, methods for fitting HGLMs in major statistical software packages permit the inclusion of more than one source of clustering or the inclusion of more than one set of random effects. When fitting a multilevel Cox model with mixed effects, not all major statistical software packages currently permit the inclusion of more than one set of random effects. However, this is possible in R (e.g. when using the coxme or frailtypack packages).
Multilevel data structures abound across a wide range of fields of research. Time‐to‐event outcomes occur frequently in many of these fields. Conventional survival models do not permit the analyst to account for the loss of independence that arises from the clustering of subjects in higher level units. Multilevel survival models permit researchers to make valid inferences when examining the effect of both subject characteristics and cluster characteristics on the risk of the occurrence of the outcome.
Les références
Source de l’article
